Qaekwy Python

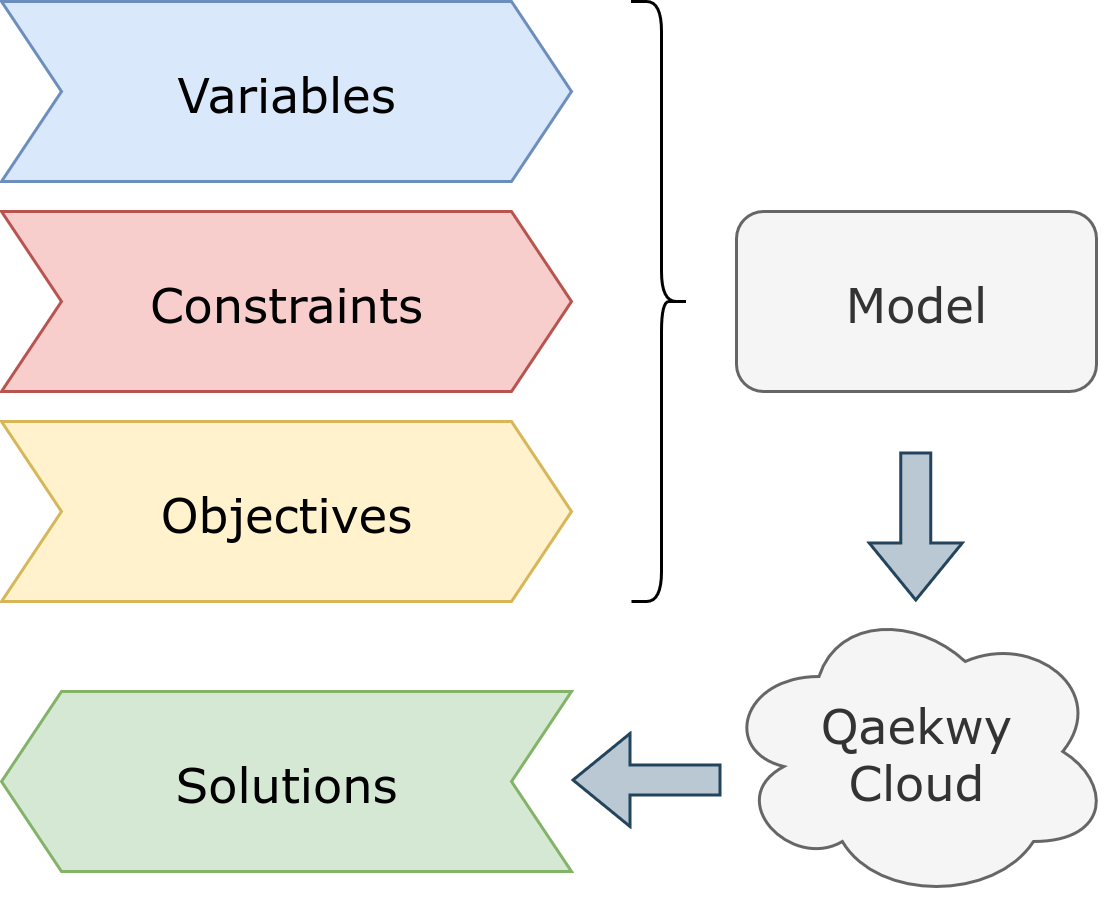
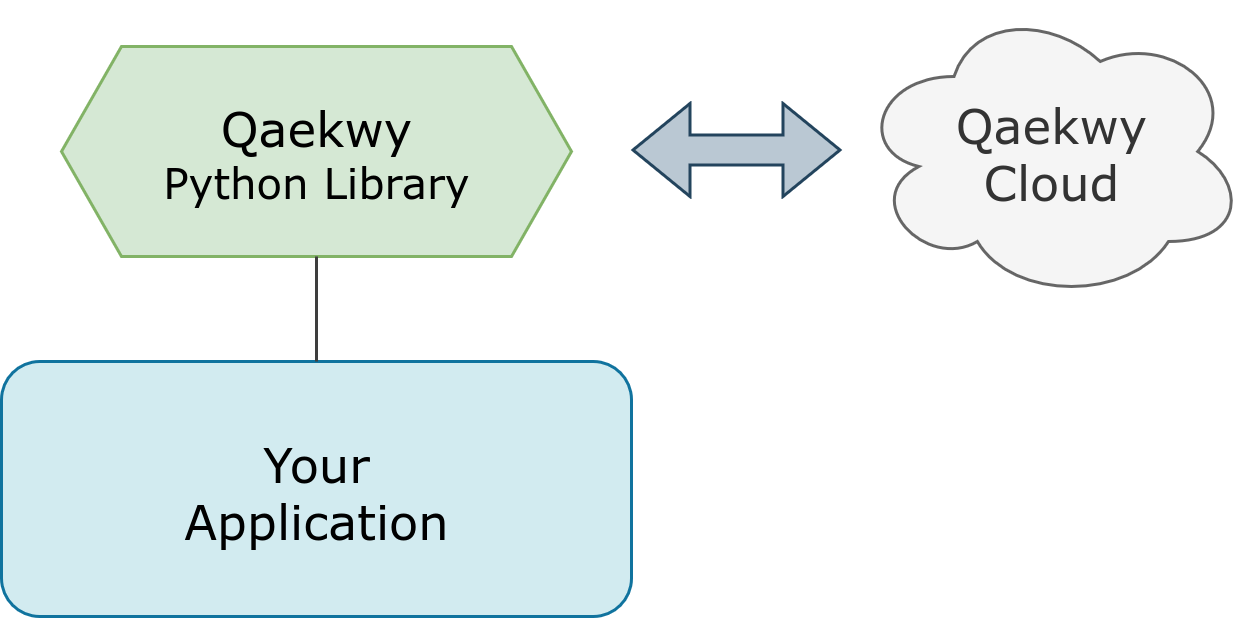
A modern, open-source Python framework for declarative constraint programming and combinatorial optimization.

Overview

Qaekwy is a Python library designed for modeling and solving combinatorial optimization and constraint satisfaction problems.

It provides a clean, Pythonic interface for defining variables, constraints, and objectives, enabling a natural define-and-solve workflow. Qaekwy manages the interaction with the solver engine, allowing users to focus entirely on expressing the structure of their problems.

Perfect for:

• 🎓 Learning: Students can quickly model and solve problems.
• 👩‍🏫 Teaching: Instructors can demo core CSP concepts with minimal setup.
• 🌟 Discovering: Researchers can explore strategies, heuristics, and models.

🚀 Quick Start

Prerequisites

• Python 3.9+
• pip

Installation

Install the production-ready client via PyPI:

pip install qaekwy

Your First Model

import qaekwy as qw

m = qw.Model()

x = m.integer_variable("x", (-10, 10))
y = m.integer_variable("y", (-10, 10))
z = m.integer_variable("z", (-10, 10))

m.constraint(x + 2*y + 3*z <= 15)
m.constraint(x + y >= 5)

m.minimize(z)

solution = m.solve_one()
solution.pretty_print()

Output:

----------------------------------------
Solution:
----------------------------------------
x: 6
y: 8
z: -3
----------------------------------------

That's it.

Capabilities

• Declarative Modeling Define integer, float, and boolean variables, as well as arrays and matrices, to represent problems at a high semantic level.
• Expressive Constraints Formulate arithmetic, logical, and conditional constraints using readable and maintainable Python expressions.
• Optimization Objectives Specify minimization and maximization goals to guide the solver toward optimal solutions.
• Search Configuration Configure solver behavior using explicit search strategies such as Depth-First Search and Branch-and-Bound, along with branching heuristics and cutoffs.
• Cloud-Native Execution Transparent handling of model serialization and execution on the Qaekwy Cloud Solver instance.

📚 Documentation

Visit the Qaekwy Documentation for guides, teaching resources, and detailed examples.

---

🧩 Constraint Programming Example: Sudoku

Here is a complete example solving a Sudoku grid:

import qaekwy as qw

# Initial Sudoku grid; 0 represents empty cells to be assigned by Qaekwy
my_problem = [
    [0, 7, 0,  0, 0, 0,  6, 9, 0],
    [0, 0, 0,  6, 1, 0,  0, 0, 0],
    [0, 9, 2,  0, 0, 0,  0, 5, 0],

    [0, 0, 0,  0, 8, 1,  7, 0, 9],
    [4, 0, 0,  0, 0, 3,  0, 0, 0],
    [0, 0, 0,  0, 5, 6,  1, 0, 8],

    [0, 5, 9,  0, 0, 0,  0, 1, 0],
    [0, 0, 0,  5, 6, 0,  0, 0, 0],
    [0, 2, 0,  0, 0, 0,  5, 7, 0]
]

# Initialize the model container
m = qw.Model()

# Create a 9x9 matrix of integer variables
# Each variable can take a value between 1 and 9 (inclusive)
grid = m.integer_matrix("grid", rows=9, cols=9, domain=(1, 9))

for i in range(9):
    # Ensure all variables in row 'i' are unique
    m.constraint_distinct(grid.row(i))
    
    # Ensure all variables in column 'i' are unique
    m.constraint_distinct(grid.col(i))

# Iterate in steps of 3 (0, 3, 6) to find the top-left corner of each block
for i in range(0, 9, 3):
    for j in range(0, 9, 3):
        # Extract the 3x3 block and enforce uniqueness
        m.constraint_distinct(grid.slice(i, j, i + 3, j + 3))

for i in range(9):
    for j in range(9):
        # If the cell is not empty (0 represents empty in our data)
        if my_problem[i][j] != 0:
            # Constrain the model variable at [i][j] to equal the input value
            m.constraint(grid[i][j] == my_problem[i][j])

# Solve the model and retrieve the first valid solution found
s = m.solve_one()

# Display the result
s.pretty_print()

Output:

----------------------------------------
Solution:
----------------------------------------
grid: (9 x 9 matrix)
    1 7 8 3 2 5 6 9 4
    5 4 3 6 1 9 8 2 7
    6 9 2 7 4 8 3 5 1
    2 6 5 4 8 1 7 3 9
    4 8 1 9 7 3 2 6 5
    9 3 7 2 5 6 1 4 8
    7 5 9 8 3 2 4 1 6
    3 1 4 5 6 7 9 8 2
    8 2 6 1 9 4 5 7 3
----------------------------------------

🎒 Optimization Example: Knapsack Problem

Here is a complete example solving a basic resource allocation problem (The Knapsack Problem):

Given a set of items, each with a weight and a value, determine which items to include in the collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.

import qaekwy as qw

# 1. Setup the Model
m = qw.Model()

weights = [2, 3, 4, 5]
values  = [3, 4, 5, 6]
limit   = 7
n_items = len(weights)

# 2. Define Decision Variables (0 = exclude, 1 = include)
selected = [
    m.integer_variable(f"item_{i}", domain=(0, 1))
    for i in range(n_items)
]

# 3. Apply Constraints
# Total weight must not exceed the limit
current_weight = sum(weights[i] * selected[i] for i in range(n_items))
m.constraint(current_weight <= limit)

# 4. Define Objective
# Maximize total value
total_value = m.integer_variable(
    name="total_value",
    expression=sum(values[i] * selected[i] for i in range(n_items)),
    branch_val=qw.BranchIntegerVal.VAL_MAX # Forces the solver to try higher values first
)
m.maximize(total_value)

# 5. Solve
solution = m.solve_one(searcher="bab") # Branch-and-Bound

print(f"Max Value: {solution.total_value}")
# Output: Max Value: 9

💡 Core Concepts

The Model

The qw.Model acts as the container for your variables and constraints. It also manages the interaction with the underlying solver engine.

The Variables

Here are examples of variable creation in the model:

# A single integer between 0 and 100
capacity = m.integer_variable("capacity", domain=(0, 100))

# A 9x9 Grid (Matrix) for Sudoku-like problems
grid = m.integer_matrix("grid", rows=9, cols=9, domain=(1, 9))

The Constraints

Constraints are logical assertions that must be true in any valid solution.

# Arithmetic
m.constraint(x * 2 < qw.math.power(y, 2) + 5)

Modeling Capabilities

Qaekwy supports:

• Conditional constraints

m.constraint_if_then_else(
    condition=x + y <= 7,
    then_constraint=z >= 2,
    else_constraint=z <= 2
)

• Logical expressions

m.constraint(
    (qw.math.absolute(z) == qw.math.power(x-(y+1),2)) | (z >= 4)
)

• Arrays and Matrices

arr = m.integer_array("arr", 3, (0,100))
m.constraint(arr[1] < x + 1)

mat = m.integer_matrix("mat", rows=2, cols=3, domain=(0,50))
m.constraint(sum(mat.col(0)) > arr[2])

...and more, visit the Qaekwy Documentation

Solving & Execution

• solve_one() — find one feasible or optimal solution
• solve() — returns a list of solutions
• minimize(...) / maximize(...) — Set one or more objectives on variables
• Searchers such as DFS, Branch-and-Bound, etc.
• Cloud-based Solver instance (please, refer to Terms & Conditions)

Integration

The model is then sent to the Qaekwy Cloud Engine through REST API.

---

License

• Released under the European Union Public Licence 1.2 (EUPL 1.2).
• Qaekwy Cloud Instance Terms & Conditions.